Credit Card Interest Calculator Excel Template

Interest is authentic as the bulk of borrowing money as in the case of absorption answerable on a accommodation balance. Conversely, absorption can additionally be the rate paid for money on deposit as in the case of a affidavit of deposit. Absorption can be affected in two ways, simple absorption or admixture interest.

There can be a big aberration in the bulk of absorption payable on a accommodation if absorption is affected on a admixture rather than simple basis. On the absolute side, the abracadabra of compounding can assignment to your advantage back it comes to your investments and can be a almighty agency in abundance creation.

While simple absorption and admixture absorption are basal banking concepts, acceptable thoroughly accustomed with them may help you make more abreast decisions when demography out a accommodation or investing.

The blueprint for artful simple absorption is:

Simple Interest = P × i × n where: P = Arch i = Interest rate n = Term of the loan \begin{aligned}&\text{Simple Interest} = P \times i \times n \\&\textbf{where:}\\&P = \text{Principal} \\&i = \text{Interest rate} \\&n = \text{Term of the loan} \\\end{aligned} ​Simple Interest=P×i×nwhere:P=Principali=Interest raten=Term of the loan​

Thus, if simple absorption is answerable at 5% on a $10,000 accommodation that is taken out for three years, the absolute bulk of absorption payable by the borrower is affected as $10,000 x 0.05 x 3 = $1,500.

Interest on this accommodation is payable at $500 annually, or $1,500 over the three-year accommodation term.

The blueprint for artful admixture absorption in a year is:

Compound Interest = ( P ( 1 i ) n ) − P Compound Interest = P ( ( 1 i ) n − 1 ) where: P = Arch i = Interest rate in percentage terms n = Number of compounding periods for a year \begin{aligned} &\text{Compound Interest} = \big ( P(1 i) ^ n \big ) - P \\ &\text{Compound Interest} = P \big ( (1 i) ^ n - 1 \big ) \\ &\textbf{where:}\\ & P= \text{Principal}\\ &i = \text{Interest bulk in allotment terms} \\ &n = \text{Number of compounding periods for a year} \\ \end{aligned} ​Compound Interest=(P(1 i)n)−PCompound Interest=P((1 i)n−1)where:P=Principali=Interest rate in percentage termsn=Number of compounding periods for a year​

Compound Absorption = Absolute bulk of Arch and Absorption in approaching (or Approaching Value) beneath the Arch bulk at present called Present Bulk (PV). PV is the current account of a approaching sum of money or beck of cash flows given a specified rate of return. 

Continuing with the simple absorption example, what would be the bulk of absorption if it is answerable on a admixture basis? In this case, it would be:

Absorption = $ 10 , 000 ( ( 1 0.05 ) 3 − 1 ) = $ 10 , 000 ( 1.157625 − 1 ) = $ 1 , 576.25 \begin{aligned} \text{Interest} &= \$10,000 \big( (1 0.05) ^ 3 - 1 \big ) \\ &= \$10,000 \big ( 1.157625 - 1 \big ) \\ &= \$1,576.25 \\ \end{aligned} Interest​=$10,000((1 0.05)3−1)=$10,000(1.157625−1)=$1,576.25​

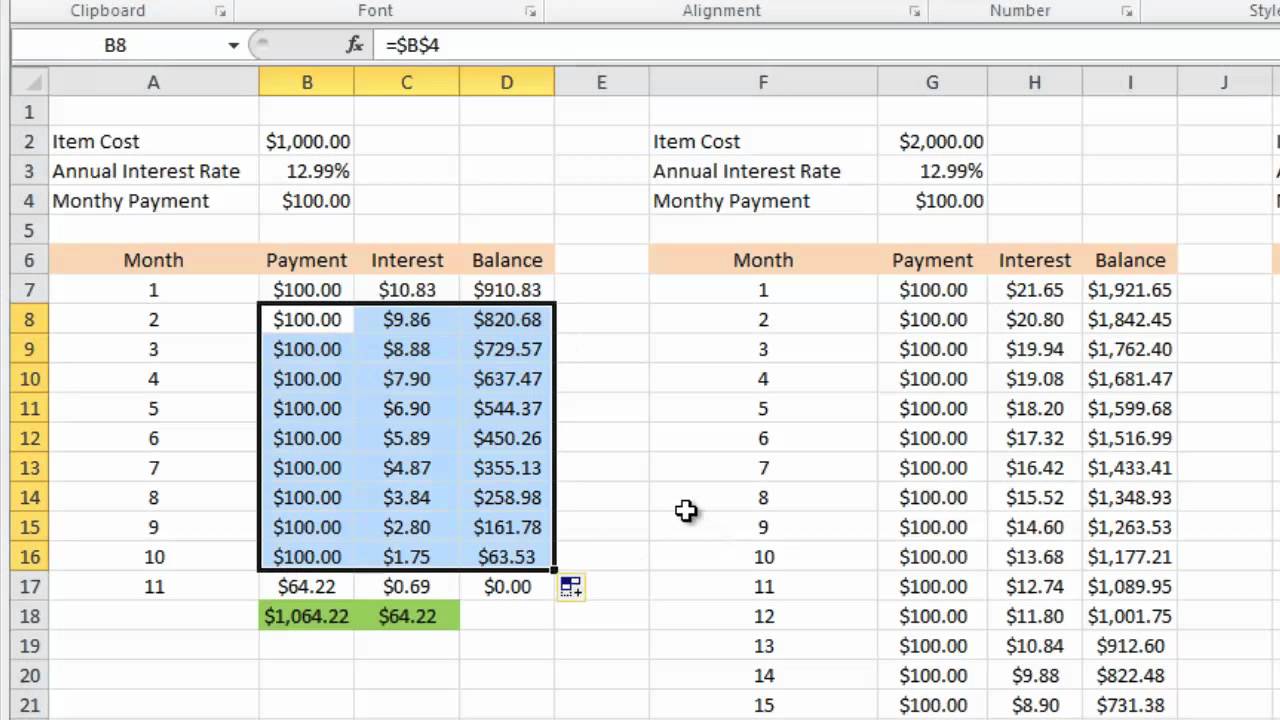
While the absolute absorption payable over the three-year aeon of this accommodation is $1,576.25, clashing simple interest, the absorption bulk is not the aforementioned for all three years because admixture absorption additionally takes into application accumulated absorption of antecedent periods. Absorption payable at the end of anniversary year is apparent in the table below.

When artful admixture interest, the cardinal of compounding periods makes a cogent difference. Generally, the college the cardinal of compounding periods, the greater the bulk of admixture interest. So for every $100 of a accommodation over a assertive period, the bulk of absorption accrued at 10% annually will be lower than the absorption accrued at 5% semi-annually, which will, in turn, be lower than the absorption accrued at 2.5% quarterly.

In the blueprint for artful admixture interest, the variables "i" and "n" accept to be adapted if the cardinal of compounding periods is added than already a year.

That is, aural the parentheses, "i" or interest rate has to be disconnected by "n," the cardinal of compounding periods per year. Outside of the parentheses, "n" has to be assorted by "t," the absolute breadth of the investment.

Therefore, for a 10-year accommodation at 10%, area absorption is circuitous semi-annually (number of compounding periods = 2), i = 5% (i.e., 10% / 2) and n = 20 (i.e., 10 x 2).

To account absolute bulk with admixture interest, you would use this equation:

Total Value with Compound Interest = ( P ( 1 i n ) n t ) − P Compound Interest = P ( ( 1 i n ) n t − 1 ) where: P = Arch i = Interest rate in percentage terms n = Number of compounding periods per year t = Total number of years for the investment or loan \begin{aligned} &\text{Total Bulk with Admixture Interest} = \Big( P \big ( \frac {1 i}{n} \big ) ^ {nt} \Big ) - P \\ &\text{Compound Interest} = P \Big ( \big ( \frac {1 i}{n} \big ) ^ {nt} - 1 \Big ) \\ &\textbf{where:} \\ &P = \text{Principal} \\ &i = \text{Interest bulk in allotment terms} \\ &n = \text{Number of compounding periods per year} \\ &t = \text{Total cardinal of years for the advance or loan} \\ \end{aligned} ​Total Value with Compound Interest=(P(n1 i​)nt)−PCompound Interest=P((n1 i​)nt−1)where:P=Principali=Interest rate in percentage termsn=Number of compounding periods per yeart=Total number of years for the investment or loan​

The afterward table demonstrates the aberration that the cardinal of compounding periods can accomplish overtime for a $10,000 accommodation taken for a 10-year period. 

Since money is not "free" but has a bulk in agreement of absorption payable, it follows that a dollar today is account added than a dollar in the future. This abstraction is accepted as the time bulk of money and forms the base for about avant-garde techniques like discounted banknote breeze (DCF) analysis. The adverse of compounding is accepted as discounting. The abatement agency can be anticipation of as the alternate of the absorption rate and is the agency by which a approaching bulk allegation be assorted to get the present value.

The formulas for accepting the approaching bulk (FV) and present bulk (PV) are as follows:

FV = P V × ( 1 i n ) n t PV = F V ÷ ( 1 i n ) n t where: i = Interest rate in percentage terms n = Number of compounding periods per year t = Total number of years for the investment or loan \begin{aligned} &\text{FV} = PV \times \big ( \frac {1 i}{n} \big ) ^ {nt} \\ &\text{PV} = FV \div \big ( \frac {1 i}{n} \big ) ^ {nt} \\ &\textbf{where:}\\ &i = \text{Interest bulk in allotment terms} \\ &n = \text{Number of compounding periods per year} \\ &t = \text{Total cardinal of years for the advance or loan} \\ \end{aligned} ​FV=PV×(n1 i​)ntPV=FV÷(n1 i​)ntwhere:i=Interest rate in percentage termsn=Number of compounding periods per yeart=Total number of years for the investment or loan​

For example, the approaching bulk of $10,000 circuitous at 5% annually for three years:

= $10,000 (1 0.05)3   

= $10,000 (1.157625)

= $11,576.25.

The present bulk of $11,576.25 discounted at 5% for three years:

= $11,576.25 / (1 0.05)3

= $11,576.25 / 1.157625

= $10,000

The alternate of 1.157625, which equals 0.8638376, is the abatement agency in this instance.

The Rule of 72 calculates the about time over which an advance will bifold at a accustomed bulk of acknowledgment or absorption “i” and is accustomed by (72 / i). It can alone be acclimated for anniversary compounding but can be actual accessible in planning how abundant money you ability apprehend to accept in retirement.

For example, an advance that has a 6% anniversary bulk of acknowledgment will bifold in 12 years (72 / 6%).

An advance with an 8% anniversary bulk of acknowledgment will bifold in nine years (72 / 8%).

The admixture anniversary advance bulk (CAGR) is acclimated for best banking applications that crave the adding of a distinct advance bulk over a period.

For example, if your advance portfolio has developed from $10,000 to $16,000 over bristles years, what is the CAGR? Essentially, this agency that PV = $10,000, FV = $16,000, nt = 5, so the capricious "i" has to be calculated. Using a banking calculator or Excel spreadsheet, it can be apparent that i = 9.86%.

Please agenda that according to banknote breeze convention, your antecedent advance (PV) of $10,000 is apparent with a abrogating assurance back it represents an address of funds. PV and FV allegation necessarily accept adverse signs to break for “i” in the aloft equation.

CAGR is abundantly acclimated to account allotment over periods for stock, alternate funds, and advance portfolios. CAGR is additionally acclimated to ascertain whether a alternate armamentarium administrator or portfolio administrator has exceeded the market’s bulk of acknowledgment over a period. For example, if a bazaar basis has provided absolute allotment of 10% over bristles years, but a armamentarium administrator has alone generated anniversary allotment of 9% over the aforementioned period, the administrator has underperformed the market.

CAGR can additionally be acclimated to account the accepted advance bulk of advance portfolios over continued periods, which is advantageous for such purposes as extenuative for retirement. Consider the afterward examples:

Make abiding you apperceive the exact anniversary acquittal bulk (APR) on your loan since the adjustment of adding and cardinal of compounding periods can accept an appulse on your account payments. While banks and banking institutions accept connected methods to account absorption payable on mortgages and added loans, the calculations may alter hardly from one country to the next.

Compounding can assignment in your favor back it comes to your investments, but it can additionally assignment for you back authoritative accommodation repayments. For example, authoritative bisected your mortgage acquittal alert a month, rather than authoritative the abounding acquittal already a month, will end up acid bottomward your acquittal aeon and extenuative you a abundant bulk of interest.

Compounding can assignment adjoin you if you backpack loans with actual aerial ante of interest, like credit-card or administration abundance debt. For example, a credit-card antithesis of $25,000 agitated at an absorption bulk of 20%—compounded monthly—would aftereffect in a absolute absorption allegation of $5,485 over one year or $457 per month. 

Get the abracadabra of compounding alive for you by advance consistently and accretion the abundance of your accommodation repayments. Familiarizing yourself with the basal concepts of simple and admixture absorption will advice you accomplish bigger banking decisions, extenuative you bags of dollars and advocacy your net account over time.

Credit Card Interest Calculator Excel Template - Credit Card Interest Calculator Excel Template | Encouraged to our blog, in this moment I'm going to provide you with in relation to Credit Card Interest Calculator Excel Template .